Civil Engineering (construction)
Page 1 of 1
 Civil Engineering (construction)
Civil Engineering (construction)
I wrote something about the math of the strength (bending moment) of pipes:
http://www.physicsforums.com/showthread.php?p=2628095#post2628095
I did notice for example that thin-walled pipes (Schedule 5) fetch 10% premium over thicker walled (Sched 10), but this outweighed by the mathematical advantage.
http://www.physicsforums.com/showthread.php?p=2628095#post2628095
I did notice for example that thin-walled pipes (Schedule 5) fetch 10% premium over thicker walled (Sched 10), but this outweighed by the mathematical advantage.
Last edited by Shelby on Wed Mar 17, 2010 1:51 pm; edited 1 time in total
 Pine is as strong as steel by weight, except for pulling, cross-grain compression, and shear strength
Pine is as strong as steel by weight, except for pulling, cross-grain compression, and shear strength
Wood (e.g. pine) is as strong as steel by weight for compression parallel to grain (as a vertical beam) and bending moment (E), but not for perpendicular-to-grain compression, shear, and tensile (pulling) strength. And wood occupies 20 times more volume. Wood is thus superior when the equivalent steel would be too thin or dense to work with (e.g. purlens to which corrugated roof is screw or nailed to).
 Most efficient shape is Pipe for 360 degree, and I-beam for uni-directional, bending strength
Most efficient shape is Pipe for 360 degree, and I-beam for uni-directional, bending strength
http://en.wikipedia.org/w/index.php?title=Beam_%28structure%29&oldid=344521000#General_shapes
Efficiency means that for the same cross sectional area (Volume of beam per length) subjected to the same loading conditions, the beam deflects less. Thus, efficiency means lowest mass and thus hopefully cost, if material mass is the most significant variable component of cost. For example (see 1st post of this thread) I did notice for example that thin-walled pipes (Schedule 5) fetch 10% premium over thicker walled (Sched 10), but this outweighed by the mathematical advantage.
Note this is because the circle is 3Pi x 4/Pi = 12 times more efficient 2nd moment of inertia than the cube (3Pi from ratios of 2nd moment of inertia and 4/Pi from ratio of areas):
http://en.wikipedia.org/wiki/List_of_area_moments_of_inertia
With cube the 2nd moment of inertia improves by a factor of 4, with bending off-axis from the centroid of the symmetry (area), which the I-beam (1 lss side than square) exploits to be the most efficient shape for uni-direction bending strength (assuming the I is at least 2 times taller than H is otherwise circle/pipe is):
http://en.wikipedia.org/wiki/Second_moment_of_area#.22I-beam.22_cross_section
"An I-beam is only the most efficient shape in one direction of bending: up and down looking at the profile as an I. When bent side-to-side, it functions as an H where it is less efficient. The most efficient shape for both directions in 2D is a box (a square shell) however the most efficient shape for bending in any direction is a cylindrical shell or tube."
Efficiency means that for the same cross sectional area (Volume of beam per length) subjected to the same loading conditions, the beam deflects less. Thus, efficiency means lowest mass and thus hopefully cost, if material mass is the most significant variable component of cost. For example (see 1st post of this thread) I did notice for example that thin-walled pipes (Schedule 5) fetch 10% premium over thicker walled (Sched 10), but this outweighed by the mathematical advantage.
Note this is because the circle is 3Pi x 4/Pi = 12 times more efficient 2nd moment of inertia than the cube (3Pi from ratios of 2nd moment of inertia and 4/Pi from ratio of areas):
http://en.wikipedia.org/wiki/List_of_area_moments_of_inertia
With cube the 2nd moment of inertia improves by a factor of 4, with bending off-axis from the centroid of the symmetry (area), which the I-beam (1 lss side than square) exploits to be the most efficient shape for uni-direction bending strength (assuming the I is at least 2 times taller than H is otherwise circle/pipe is):
http://en.wikipedia.org/wiki/Second_moment_of_area#.22I-beam.22_cross_section
 Concrete design
Concrete design
Light-weight polystyrene concrete:
http://www.najah.edu/researches/226.pdf
Slump test is for other mixes (optimum water is critical for max strength and minimum cracks):
 <--click for source
<--click for source
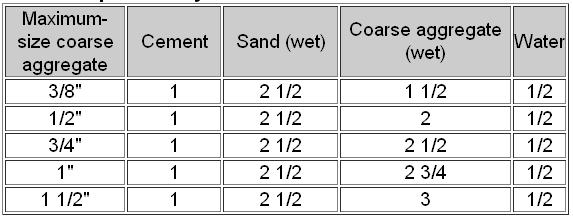
If sand is wet and depending humidity, this can affect how much water we should add. Density of Portland cement is roughly the same as DRY sand or gravel, so equal mix is same volume of sand to cement. For footers a 1-2-3 volume mix of cement, DRY sand, gravel is advised. Sand with sharp edges (wedges instead of balls) is best, so river sand not ocean sand.
The concrete will typically be 2/3 of the volume of the mix aggregates. So a cu.yard is 27 cu.ft, so we need 40.5 cu.ft of aggregates. Since a 94lb bag of Portland cement is roughly a cu.ft., then for a 1-2-3 mix, we need 6.75 bags of cement, 13.5 bags of sand, 20.25 bags gravel. Water is 40 - 60% of the Portland cement (if all aggregates are dry), but has to be adjusted to slump test. Remember water density is 1000kg/cu.meter and density of portland cement is 1500kg/cu.m, so 50% of water to cement ratio by weight would be 75% by volume.
http://www.concretenetwork.com/concrete/slabs/ratio.htm
http://www.fao.org/docrep/s1250e/S1250E08.htm
http://en.wikipedia.org/wiki/Water%E2%80%93cement_ratio
http://www.bulgarianbuildingservices.com/how-tos/how-to-mix-concrete/
http://en.wikipedia.org/wiki/Types_of_concrete#Regular_concrete
http://ezinearticles.com/?The-Two-Most-Important-DIY-Concrete-Mix-Recipes&id=2058818
http://www.diy-extra.co.uk/concrete_and_mortar_guide.html
http://www.creativehomeowner.com/index.php?pane=project&projectid=chmas114
http://www.lifewater.ca/Appendix_J.htm
http://www.cement.org/basics/concretebasics_aggregate.asp
http://www.cement.org/tech/faq_cement.asp
http://www.the-anglo-french-forum.co.uk/index.php?topic=2787.0
http://www.diy-forum.net/structural-concrete-mix-t4168.html
http://www.najah.edu/researches/226.pdf
Slump test is for other mixes (optimum water is critical for max strength and minimum cracks):
 <--click for source
<--click for sourceIf sand is wet and depending humidity, this can affect how much water we should add. Density of Portland cement is roughly the same as DRY sand or gravel, so equal mix is same volume of sand to cement. For footers a 1-2-3 volume mix of cement, DRY sand, gravel is advised. Sand with sharp edges (wedges instead of balls) is best, so river sand not ocean sand.
The concrete will typically be 2/3 of the volume of the mix aggregates. So a cu.yard is 27 cu.ft, so we need 40.5 cu.ft of aggregates. Since a 94lb bag of Portland cement is roughly a cu.ft., then for a 1-2-3 mix, we need 6.75 bags of cement, 13.5 bags of sand, 20.25 bags gravel. Water is 40 - 60% of the Portland cement (if all aggregates are dry), but has to be adjusted to slump test. Remember water density is 1000kg/cu.meter and density of portland cement is 1500kg/cu.m, so 50% of water to cement ratio by weight would be 75% by volume.
http://www.concretenetwork.com/concrete/slabs/ratio.htm
Strength improves with lower water cement ratios. A .45 water cement ratio most likely will hit 4500 psi (pounds per square inch) or greater. A .50 water cement ratio will likely reach 4000 psi or greater.
Concrete which is moist cured for 7 days is about 50% stronger than concrete exposed to dry air for the same period.
http://www.fao.org/docrep/s1250e/S1250E08.htm
Table 3.11 Typical Strength Development of Concrete
Average crushing strength
Ordinary Portland cement(1 cement - 6 aggregate, by weight, 0.60 water - cement ratio).
Age at test Storage in air 18°C 65%, R H N/mm2 Storage in water N/mm2 1 day 5.5 - 3 days 15.0 15.2 7 days 22.0 22.7 28 days 31.0 34.5 3 months 37.2 44.1
http://en.wikipedia.org/wiki/Water%E2%80%93cement_ratio
For every pound (or kilogram or any unit of weight) of cement, about 0.25 pounds (or 0.25 kg or corresponding unit) of water is needed to fully complete the hydration reactions. This requires a water-cement ratio of 1:4 often given as a proportion: 0.25. However, a mix with a w/c ratio of 0.25 may not mix thoroughly, and may not flow well enough to be placed, so more water is used than is technically necessary to react with the cement. More typical water-cement ratios of 0.4 to 0.6 are used. For higher-strength concrete, lower water:cement ratios are used, along with a plasticizer to increase flowability.
http://www.bulgarianbuildingservices.com/how-tos/how-to-mix-concrete/
Cement : Sand : Gravel
1 : 2 : 5 for grade C15(general purpose concrete)
1 : 2 : 4 for grade C25(strong)
1 : 2 : 3 for grade C30(very strong)
The usual required strenght of the concrete are:
For C30: 30 Megapascal(N/mm2)=4351 psi = 305 kg/m2;generally 4500 psi
For C25: 25 MP (N/mm2) = 3625 psi = 255 kg/m2; generally 4000 psi
For C20: 20 MP (N/mm2) = 2900 psi = 203 kg/m2; gen. 3000 psi
For C15: 15 MP (N/mm2) = 2175 psi = 152 kg/m2; gen. 2000 psi
http://en.wikipedia.org/wiki/Types_of_concrete#Regular_concrete
Typically, a batch of concrete can be made by using 1 part Portland cement, 2 parts dry sand, 3 parts dry stone, 1/2 part water. The parts are in terms of weight – not volume. For example, 1-cubic-foot (0.028 m3) of concrete would be made using 22 lb (10.0 kg) cement, 10 lb (4.5 kg) water, 41 lb (19 kg) dry sand, 70 lb (32 kg) dry stone (1/2" to 3/4" stone). This would make 1-cubic-foot (0.028 m3) of concrete and would weigh about 143 lb (65 kg). The sand should be mortar or brick sand (washed and filtered if possible) and the stone should be washed if possible. Organic materials (leaves, twigs, etc.) should be removed from the sand and stone to ensure the highest strength.
http://ezinearticles.com/?The-Two-Most-Important-DIY-Concrete-Mix-Recipes&id=2058818
The best overall mix for a DIY enthusiast to memorize and use is a simple 3:1 mortar mix. By using three parts sand and one part mortar you can create the strongest concrete possible as well as concrete that is easy to finish and detail with designs, templates or stamps. By not using the gravel the mortar will have a smoother overall consistency, but will ultimately occupy less volume than concrete made using gravel as well. If you are pouring very large volumes of concrete the gravel could prove to be cost effective however for most DIY projects a 3:1 mortar mix is the way to go.
http://www.diy-extra.co.uk/concrete_and_mortar_guide.html
General Purpose Concrete – 1:2:3 mix
Ideal for most uses except foundations and exposed paving. It is composed of one part cement, two parts sand and three parts coarse aggregate. If using combined aggregate, this mix would be 1:4, one part cement to four parts combined aggregate.
Foundation Concrete – 1:2 ½:3 ½ mix
Ideal for wall foundations or bases and laying paving slabs, etc. One part cement, two and a half sand and three and a half coarse aggregate. If using combined aggregate, this mix would be 1:5.
Paving Concrete – 1:1 ½:2 ½ mix
Used for exposed paving such as driveways and garage floors. One part cement, one and a half parts sand and two and a half parts coarse aggregate. Combined aggregate would need a mix of 1:3 ½.
http://www.creativehomeowner.com/index.php?pane=project&projectid=chmas114
2. Using a Power Mixer
The size of the concrete batch is usually only about 60 percent of the total capacity of the mixer to allow room for proper mixing without spilling. Never load a mixer beyond its maximum batch size.
Be sure to use the correct proportions of concrete ingredients. For best results, follow this procedure: With the mixer stopped, add all the coarse aggregate and half the water. Start the mixer; then add the sand, cement, and remaining water. After all ingredients are in the drum, continue mixing for at least three minutes or until the ingredients are thoroughly mixed and the concrete has a uniform color.
Thoroughly clean the mixer as soon as you have finished using it. Place water and a few shovelfuls of coarse aggregate into the drum while it is turning, to scour the inside of the mixer. Then dump out the water and gravel, and hose out the drum.
http://www.lifewater.ca/Appendix_J.htm
Reinforced concrete should be at least 7.5 cm thick. Rerod should take up 0.5% to 1% of the cross-sectional area. The rebar should be placed within the concrete form and be located at least 2 cm from the edge of the form. It should be placed in a grid pattern so that there is never more than 3 times the final concrete thickness between adjacent rods. (With a final thickness of 10 cm use a grid spacing of 25 cm)
http://www.cement.org/basics/concretebasics_aggregate.asp
Shape and Size Matter
Particle shape and surface texture influence the properties of freshly mixed concrete more than the properties of hardened concrete. Rough-textured, angular, and elongated particles require more water to produce workable concrete than smooth, rounded compact aggregate. Consequently, the cement content must also be increased to maintain the water-cement ratio. Generally, flat and elongated particles are avoided or are limited to about 15 percent by weight of the total aggregate. Unit-weight measures the volume that graded aggregate and the voids between them will occupy in concrete. The void content between particles affects the amount of cement paste required for the mix. Angular aggregate increase the void content. Larger sizes of well-graded aggregate and improved grading decrease the void content.
http://www.cement.org/tech/faq_cement.asp
http://www.the-anglo-french-forum.co.uk/index.php?topic=2787.0
Here are some ratios for Concrete Mixes:
C7.5 (low strength) 1:3:6 or7 (Cement/Sand/Coarse Aggregate)
For general non-structural use – bedding in kerbs, posts, stabilising underground pipes etc.
C10 to C15 (medium strength) 1:4:6 to 1:4:5 (Cement/Sand/Medium Aggregate)
Used in typical house foundations, footings for garden walls, load-bearing areas etc.
C20 (strong) 1:2:4 (Cement/Sand/Medium Aggregate)
Used as a footing mix in house construction in softer ground. Also as the slab foundation to floors, bases for caravans and pathways, hard landscaping.
C25 (stronger) 1:1.5:3 (Cement/Sand/Medium Aggregate)
Can be used for foundations to larger houses and for creating floors. Can also take light traffic. Also suitable for lining pools and fosse septic.
C30 (very strong) 1:2:3 (Cement/Sand/Fine Aggregate)
A general-purpose, easy-to-remember mix for many hard-wearing applications.
C35 (industrial strength) 1:1.5:2.5 (Cement/Sand/Fine Aggregate)
Structural concrete for major construction work and roadways
C40/45 (atomic bunkers) Major civil engineering projects, bridges, skyscrapers and unlikely to be needed for domestic use!
http://www.diy-forum.net/structural-concrete-mix-t4168.html
What C40 means is that the characteristic strength of 100mm cubes
made, cured and testing in the standard way achieve a strength of 40
Newtons/mm^2.
Depending on the aggregates and cement used, to give you a rough idea,
the required mix would probably need to be:-
Portland cement 375kg/m^3
20 - 10 mm aggregate 690kg/m^3
10 - 5 mm aggregate 345kg/m^3
Sand 800kg/m^3
Water 187 litres
Last edited by Shelby on Tue Mar 20, 2012 8:26 pm; edited 20 times in total
 Warren Truss Design
Warren Truss Design
http://www.garrettsbridges.com/design/trussdesign
http://www.jhu.edu/virtlab/bridge/truss.htm
http://www.jhu.edu/virtlab/bridge/bridge.htm
10/1 (length/height), 5 top, 4 btm nodes:
Distributed F, 1.25F horiz & 0.6F vertical members
Concentrated F, 2.5F horiz & 1.1F vertical members
12/1 (length/height), 6 top, 5 btm nodes:
Distributed F, 1.5F horiz & 0.6F vertical members
Concentrated F, 3F horiz & 1.2F vertical members
Concentrated only inner 2 (top) & 3 (btm) most horiz members
Concentrated only outer 2 most vert members, rest at most 1F
14/1 (length/height), 7 top, 6 btm nodes:
Distributed F, 1.75F horiz & 0.6F vertical members
Concentrated F, 3.5F horiz & 1.2F vertical members
Concentrated only inner 3 (top) & 4 (btm) most horiz members
Concentrated only outer 2 most vert members, rest at most 1F
20/1 (length/height), 10 top, 9 btm nodes:
Distributed F, 2.5F horiz & 0.6F vertical members
Concentrated F, 5F horiz & 1.3F vertical members
Concentrated only inner 4 (top) & 5 (btm) most horiz members
Concentrated only outer 2 most vert members, rest at most 1.1F
40/1 (length/height), 20 top, 19 btm nodes:
Distributed F, 4F horiz & 0.6F vertical members
Concentrated F, 8F horiz & 1.1F vertical members
Concentrated only inner 10 (top) & 9 (btm) most horiz members
Concentrated only outer 2 most vert members, rest at most 0.9F
F = downward load force
http://www.jhu.edu/virtlab/bridge/truss.htm
http://www.jhu.edu/virtlab/bridge/bridge.htm
10/1 (length/height), 5 top, 4 btm nodes:
Distributed F, 1.25F horiz & 0.6F vertical members
Concentrated F, 2.5F horiz & 1.1F vertical members
12/1 (length/height), 6 top, 5 btm nodes:
Distributed F, 1.5F horiz & 0.6F vertical members
Concentrated F, 3F horiz & 1.2F vertical members
Concentrated only inner 2 (top) & 3 (btm) most horiz members
Concentrated only outer 2 most vert members, rest at most 1F
14/1 (length/height), 7 top, 6 btm nodes:
Distributed F, 1.75F horiz & 0.6F vertical members
Concentrated F, 3.5F horiz & 1.2F vertical members
Concentrated only inner 3 (top) & 4 (btm) most horiz members
Concentrated only outer 2 most vert members, rest at most 1F
20/1 (length/height), 10 top, 9 btm nodes:
Distributed F, 2.5F horiz & 0.6F vertical members
Concentrated F, 5F horiz & 1.3F vertical members
Concentrated only inner 4 (top) & 5 (btm) most horiz members
Concentrated only outer 2 most vert members, rest at most 1.1F
40/1 (length/height), 20 top, 19 btm nodes:
Distributed F, 4F horiz & 0.6F vertical members
Concentrated F, 8F horiz & 1.1F vertical members
Concentrated only inner 10 (top) & 9 (btm) most horiz members
Concentrated only outer 2 most vert members, rest at most 0.9F
F = downward load force
 Wall Design
Wall Design
http://www.ehow.com/how_5985528_convert-wind-speed-force.html
An 8'x8' external wall exposed to a 100 MPH wind, will receive 1.5T (3000lbs) force, or proportionally for other wind speeds.
An 8'x8' external wall exposed to a 100 MPH wind, will receive 1.5T (3000lbs) force, or proportionally for other wind speeds.
 Concrete road design
Concrete road design
http://en.wikipedia.org/wiki/Road_surface#Concrete
Continuously Reinforced Concrete Pavements (CRCP) do not require any transverse contraction joints. Transverse cracks are expected in the slab, usually at intervals of 3–5 ft. CRCP pavements are designed with enough steel, 0.6–0.7% by cross-sectional area, so that cracks are held together tightly.
Continuously reinforced designs may cost slightly more than jointed reinforced or jointed plain designs due to increased quantities of steel. Often the cost of the steel is offset by the reduced cost of concrete because CRCP is nearly always significantly thinner then a JPCP designed for the same traffic loads. Properly designed JPCP and CRCP should demonstrate similar long-term performance and cost-effectiveness.
 One-way elevated concrete slab design
One-way elevated concrete slab design
A one-way concrete slab is where the width in the long direction is 2 or more times greater than the spanning length in the perpendicular direction, were the supporting beams are on each edge of the spanning length:
http://www.wikiengineer.com/Structural/ConcreteSlabDesign
http://www.cecalc.com/ConcreteFloors1way.aspx
http://faculty.kfupm.edu.sa/CE/agadhib/Note/Slab.pdf
1) For continuous supporting beam on each side (my trusses), we need the slab thickness to be (spanning length)/28. I am using 8 feet span length between trusses, so my slab must be 8x12/28 = 3.5 in or greater. I will use 4", because smaller than that makes it difficult to keep the rebar near to the bottom of the slab (important for vertical bending moment maximizing strength, see #2).
2) We design the structural steel as if we are designing a 12" width beam. Since my span length is 8', then I can calculate the weight of that beam:
8 ft x 12 in/ft x 12 in x 4 in = 4608 cu. in / (39.37 in/m) ^ 3 = 0.08 cu. meter x 2500 kg / cu.m = 189 kg x 2.2 lbs / kg = 417 lbs.
I use the following calculator to design concrete beams:
http://www.strucsoft.com/applets/BeamStrength.htm#BeamStrength
b = 12" (width of the beam)
d = 3" (rebar will be 1" from bottom of 4" beam thickness)
fc' = 3Ksi (3000 psi) concrete strength
fy = 36 ksi (36,000 psi A36 steel)
We need each edge of the beam to support the half of the weight in the center of the beam, so the minimum bending moment to hold up the weight of the beam is:
(417/2) x (96/2) = 10,000 psi = 10 Ksi
So just to hold up the weight of the concrete, we need:
As = 0.1 cu. in of rebar area
Area of circle is RxRxPi, so 12mm rebar is 3.1459 x (6/25.4) ^ 2 = 0.175 cu. in. So a 12mm rebar every 6" of width, is 2 x 0.175 = 0.35 cu. in for As. That gives us a bending moment strength of 34 Ksi. So the 12" wide section of floor can support about 900 lbs of additional weight.
The maximum spacing of the rebar is the smaller of 18" or thickness (4") x 3. So 6" spacing is okay.
3) We also need temperature steel rebar running perpendicular to the structural rebar.
http://www.wikiengineer.com/Structural/TemperatureSteel
http://www.cecalc.com/ConcreteFloors1way.aspx
So roughly 0.002 x 12" x 4" = 0.096 cu. in.
So that is 10mm spaced every 12", which is within the maximum spacing of 18" or 5 x thickness (4").
http://www.wikiengineer.com/Structural/ConcreteSlabDesign
http://www.cecalc.com/ConcreteFloors1way.aspx
http://faculty.kfupm.edu.sa/CE/agadhib/Note/Slab.pdf
1) For continuous supporting beam on each side (my trusses), we need the slab thickness to be (spanning length)/28. I am using 8 feet span length between trusses, so my slab must be 8x12/28 = 3.5 in or greater. I will use 4", because smaller than that makes it difficult to keep the rebar near to the bottom of the slab (important for vertical bending moment maximizing strength, see #2).
2) We design the structural steel as if we are designing a 12" width beam. Since my span length is 8', then I can calculate the weight of that beam:
8 ft x 12 in/ft x 12 in x 4 in = 4608 cu. in / (39.37 in/m) ^ 3 = 0.08 cu. meter x 2500 kg / cu.m = 189 kg x 2.2 lbs / kg = 417 lbs.
I use the following calculator to design concrete beams:
http://www.strucsoft.com/applets/BeamStrength.htm#BeamStrength
b = 12" (width of the beam)
d = 3" (rebar will be 1" from bottom of 4" beam thickness)
fc' = 3Ksi (3000 psi) concrete strength
fy = 36 ksi (36,000 psi A36 steel)
We need each edge of the beam to support the half of the weight in the center of the beam, so the minimum bending moment to hold up the weight of the beam is:
(417/2) x (96/2) = 10,000 psi = 10 Ksi
So just to hold up the weight of the concrete, we need:
As = 0.1 cu. in of rebar area
Area of circle is RxRxPi, so 12mm rebar is 3.1459 x (6/25.4) ^ 2 = 0.175 cu. in. So a 12mm rebar every 6" of width, is 2 x 0.175 = 0.35 cu. in for As. That gives us a bending moment strength of 34 Ksi. So the 12" wide section of floor can support about 900 lbs of additional weight.
The maximum spacing of the rebar is the smaller of 18" or thickness (4") x 3. So 6" spacing is okay.
3) We also need temperature steel rebar running perpendicular to the structural rebar.
http://www.wikiengineer.com/Structural/TemperatureSteel
http://www.cecalc.com/ConcreteFloors1way.aspx
So roughly 0.002 x 12" x 4" = 0.096 cu. in.
So that is 10mm spaced every 12", which is within the maximum spacing of 18" or 5 x thickness (4").
Page 1 of 1
Permissions in this forum:
You cannot reply to topics in this forum